Lecture
Evolution is a multi-stage process of the emergence of organic forms with a higher degree of organization, which is characterized by the variability of the evolutionary mechanisms themselves. Evolutionary modeling can be defined as reproducing the process of natural evolution using special computer programs. The necessary and sufficient conditions that determine the main factors of evolution were formulated in the 20th century. The factors that determine the inevitability of evolution include:
1) hereditary variability as a prerequisite for evolution, its material;
2) the struggle for existence as a controlling and directing factor;
3) natural selection as a transformative factor.
In fig. 10.1 shows the concretization of the factors of evolution, taking into account the diversity of the forms of their manifestation, interconnections and mutual influence. The main factors are highlighted by a dotted line.
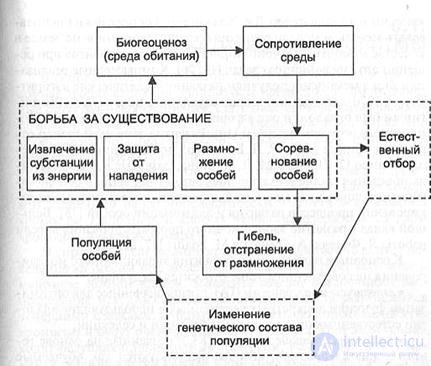
Figure 10.1 - The relationship of evolution factors.
The modern theory of evolution is based on the theory of general and population genetics. An elementary object of evolution is a population - a community of freely crossed individuals. Microevolutionary processes occur in populations, leading to changes in their gene pool. Transformations of the genetic composition of the population occur under the influence of elementary evolutionary factors. Random structural or functional changes in genes, chromosomes, and other reproducible units are called mutations if they lead to a hereditary change in any phenotypic trait of an individual. Chromosomes are specific structures of the cell nucleus, which play a crucial role in cell division processes. Chromosomes are made up of genes. The genome is called a real-life, independent, combinable and fissionable during crossing units of heredity. Gene pool transformations occur under the control of natural selection.
The history of evolutionary computing began with the development of a number of independent models, among which were genetic algorithms and classification systems created by the American researcher J. Holland. He proposed using the methods and models of the development of the organic world on Earth as a mechanism for combinatorial enumeration of variants when solving optimization problems. Computer implementations of this mechanism are called "genetic algorithms".
The main directions of development of evolutionary modeling at the present stage include the following:
- genetic algorithms (GA), designed to optimize the functions of discrete variables and using the analogies of the natural processes of recombination and selection;
- classifying systems (CS), created on the basis of genetic algorithms, which are used as trainable control systems;
- genetic programming (GP), based on the use of evolutionary methods to optimize computer programs created;
- evolutionary programming (EP), focused on the optimization of continuous functions without the use of recombinations;
- evolutionary strategies (EVS), focused on the optimization of continuous functions using recombinations.
It is advisable to use evolutionary methods in cases where an application problem is difficult to formulate in the form that allows you to find an analytical solution, or when you need to quickly find an approximate result, for example, when managing systems in real time.
A genetic algorithm is a search algorithm based on natural mechanisms of selection and genetics. These algorithms ensure the survival of the strongest solutions from the set of generated ones, forming and changing the search process based on the modeling of the evolution of the initial population of solutions. Genetic algorithms are designed in such a way that when each new population is generated, fragments of the original solutions are used, to which new elements are added that provide improved solutions for the formulated selection criteria.
When developing genetic algorithms, two main objectives are pursued:
1) an abstract and formal explanation of the adaptation processes in natural systems;
2) design of artificial software systems that reproduce the mechanisms of functioning of natural systems.
The main differences of GA from other optimization algorithms:
1) not parameters are used, but encoded sets of parameters;
2) the search is carried out not from a single point, but from a population of points;
3) in the search process, the values of the objective function are used, but not its increment;
4) probabilistic, rather than deterministic, rules for searching and generating solutions are applied;
5) simultaneous analysis of different regions of the solution space is performed, and therefore it is possible to find new regions with the best values of the objective function by combining quasi-optimal solutions from different populations.
The genetic algorithms are based on genetics and the chromosomal theory of the evolution of organisms. Classical genetics substantiated heredity and variability by creating a fundamental theory of a gene, the main points of which are formulated as follows:
1. all signs of the body are determined by sets of genes;
2. genes are elementary units of hereditary information that are located in chromosomes;
3. genes are subject to change - to mutate;
4. mutations of individual genes lead to changes in individual elemental traits of an organism, or phenes.
The terms taken from genetics are interpreted in GA as follows:
| Genetics | Genetic algorithms |
| Chromosome | Solution, string, string, sequence, parent, child |
| Population | Solution set (chromosomes) |
| Locus | The location of the gene in the chromosome |
| Gene | Element, characteristic, feature, property, detector |
| Generation | The cycle of the genetic algorithm, in the process of which many solutions are generated |
| Allele | The value of the element, characteristics |
| Epistasis |
Many parameters, alternative solutions
|
Each solution from the set of possible ones can be represented by a set of information that can be changed by introducing elements of another solution into it. In other words, the possible solutions correspond to chromosomes consisting of genes, and during the optimization, an exchange of genes between the chromosomes occurs - recombination. The recombination is used to accumulate in the final decision the best functional features that were in the set of initial solutions.
Chromosomes are filamentous structures located in the cell nucleus, which are carriers of heredity. Each chromosome is unique morphologically and genetically and cannot be replaced by another one or restored when it is lost (when a chromosome is lost, the cell usually dies). Each species has a specific, constant number of chromosomes. Each cell contains a double set of morphologically and genetically similar chromosomes. For example, in human cells contains 23 pairs of chromosomes, in mosquito cells - 3.
A gene is defined as a structural unit of hereditary information, further indivisible in functional terms. The complex of genes contained in the set of chromosomes of a single organism forms the genome.
There are several types of recombination of chromosome regions. In genetic algorithms, the most common operation of crossing-over, which consists in breaking homologous chromatids with their subsequent combination in a new combination. It leads to the emergence of a new combination of linked genes. A cross-over pattern demonstrating the formation of two new chromosomes after the exchange of genetic material is shown in Fig. 10.2. The main goal of crossing-over is to create the desired combination of traits in one solution from the available genetic material.
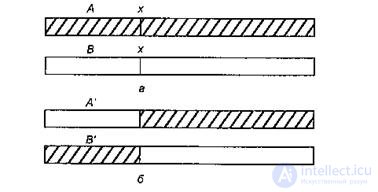
Figure 10.2 - Crossover scheme:
a) parental chromosomes before crossing-over,
b) descendant chromosomes after crossing-over.
Crossing over can occur at several points. An example of double crossing over between chromosomes is shown in fig. 10.3.
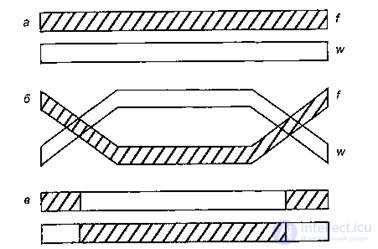
Figure 10.3 - Double crossover scheme:
a) before crossing over, b) during crossing over,
c) after crossing over.
In addition to crossing-over, genetic operations such as mutation, inversion, translocation, selection, and genetic engineering are useful for solving various applied problems.
Mutation is understood as a genetic change that leads to a qualitatively new manifestation of the basic properties of genetic material. The use of mutation operations in genetic algorithms is aimed at obtaining solutions that cannot be improved qualitatively through crossing-over.
Inversion, translocation, transposition, deletion and duplication refer to the chromosomal mutation species. With inversion, the chromosome region is rotated 180 °. Translocation refers to the transfer of parts of one chromosome to another. When moving small areas of genetic material within the same chromosome, the term transposition is used. Deletion is the loss of individual sections of chromosomes, duplication is a repetition of a section of genetic material. In addition to these, there are other types of chromosomal mutations.
According to Holland, the genetic schemes for finding optimal solutions include the following stages of the evolution process:
1. Construct the initial population. The starting point of the generations t = 0 is entered. The chromosome fitness of the population (the objective function) and the average fitness of the entire population are calculated.
2. Set the value t = t + 1. Two parents (chromosomes) are selected for crossing-over. The selection is randomly proportional to the viability of the chromosomes, which is characterized by the values of the objective function.
3. The genotype of the descendant is formed. For this, a given crossing operation is performed with a given probability over the genotypes of the selected chromosomes. One of the descendants of A (t) is randomly selected, to which inversion and mutation operators are sequentially applied with given probabilities. The resulting chromosome is stored as A '(t).
4. Update the current population by replacing a randomly selected chromosome with A '(t).
5. Determination of fitness A '(t) and recalculation of the average fitness of the population.
6. If t = t *, where t * is a given number of steps, then go to step 7, otherwise go to step 2.
7. End of work.
The basic idea of evolution, embedded in various constructs of genetic algorithms, is manifested in the ability of the “best” chromosomes to exert a greater influence on the composition of the new population due to long-term survival and more numerous offspring.
A simple genetic algorithm includes the operation of randomly generating an initial population of chromosomes and a number of operators that ensure the generation of new populations based on the initial one. These operators are reproduction, crossing over and mutation.
Reproduction is the process of chromosome copying, taking into account the values of the objective function, i.e. chromosomes with the “best” values of the objective function have a greater likelihood of entering the next population. This process is an analogy of mitotic cell division. The selection of cells (chromosomes) for reproduction is carried out in accordance with the principle of "survival of the fittest." The simplest way to represent a reproduction operation in an algorithmic form is a roulette wheel, in which each chromosome has a field proportional to the value of the objective function.
In algorithmic implementations of the chromosome reproduction mechanism, the following rules should be followed.
1. The choice of the initial population can be performed arbitrarily, for example by tossing a coin.
2. Reproduction is carried out on the basis of modeling the movement of the roulette wheel.
3. A crossover operator is implemented as a mutual exchange of short fragments of binary strings of homologous chromosomes.
4. The probability of a crossover operator is assumed to be P (CO) <1.
5. The probability of a mutation operator is assumed to be P (MO)> 0.001.
Consider an example of applying a simple genetic algorithm to maximize the function f (x) = x 2 on the integer interval [0, 31].
Values of the function argument varying from 0 to 31 can be represented by five-bit binary numbers. The initial population consisting of four five-digit numbers was obtained using the random number generation procedure.
Analysis of the initial population in the first step of a simple genetic algorithm:
| Chromosome number | X value (decimal code) | Binary chromosome code | Objective function value | Probability of choice | The expected number of copies of the chromosome in the next generation | The real number of copies of the chromosome in the next generation |
| 0.14 0.49 0.06 0.31 | 0.56 1.96 0.24 1.24 | |||||
| Amount | 1.00 | 4.00 | ||||
| Average value | 0.25 | 1.00 | ||||
| Maximum value | 0.49 | 1.97 |
The probability of choosing the i-th chromosome is calculated by the formula
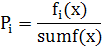
where fi (x) is the value of the objective function of the i-th chromosome in the population; sumf (x) is the total value of the objective function of all chromosomes in the population.
The expected number of copies of the i-th chromosome after the reproduction operator is equal to
N = P i n;
where n is the number of chromosomes analyzed.
The reproduction of the initial set consists of a fourfold rotation of the roulette wheel (4 is the power of the population), as a result of which the composition of the initial population may change.
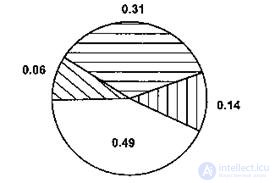
Figure 10.4 - Roulette wheel.
It should be noted that the roulette wheel does not guarantee the selection of the best chromosomes, i.e. sometimes chromosomes with low values of the objective function can be the result of a choice.
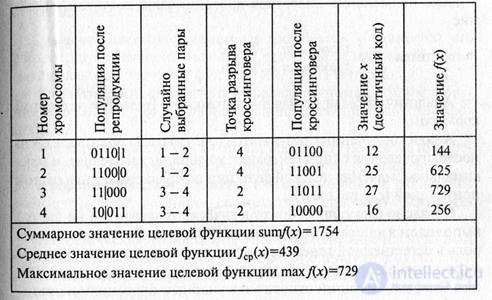
After reproduction, a cross-over statement is performed, which can be repeated several times. In this case, each time there will be a choice of two candidates from the set of chromosomes. Then each pair of chromosomes intersects. The place of intersection K is chosen randomly in the interval (1, L-1), where L is the length of the chromosome, determined by the number of significant digits in its binary code. In our case, L = 5. Two new chromosomes are created by the mutual exchange of all values after the intersection point, i.e. between the positions (K + 1) and L. When choosing the first two chromosomes from the population (see table) and K = 4 values, before applying the crossover operator, we have the following description:
chromosome1: 0110 | 1
chromosome2: 1100 | 0
After applying the crossover operator, we get the description:
chromosome1: 0110 | 0
chromosome2: 1100 | 1
Similarly, descendants from the third and fourth chromosomes were obtained.
Analysis of the obtained results shows that, after a single generation, both the average and maximum value of the objective function improved compared with the initial population.
According to the scheme of a simple genetic algorithm, in step 3, the mutation operator is executed, which plays a significant role in natural genetics and evolution, but less significant in genetic algorithms. Usually choose one mutation per 1000 bits. The mutation operator refers to unary operations and is implemented in two stages.
Step 1. On chromosome A = {a 1 , a 2 , a 3 ... a L-2 , a L-1 , a L } two positions are randomly determined, for example, 2 and L-1.
Stage 2. The genes corresponding to the selected positions are reversed and form a new chromosome A = {a 1 , a L-1 , a 3 , ..., a L-2 , a 2 , a L }
If the length of the processed sequences is small, then in the process of mutation it is possible to carry out a full search of possible gene rearrangements and find a combination with the maximum value of the objective function. Select the third chromosome 11011 with the value of the objective function f (x) = 729 and apply the mutation operation to positions 3 and 4:
chromosome 3: 11011 -> chromosome 3 ': 11101.
In the new chromosome 3 ', the value of the objective function is (29) 2 = 841. Let's make another permutation of 4 and 5 genes in chromosome 3 ':
chromosome 3 ': 11101 -> chromosome 3 ": 11110.
The value of the objective function for chromosome 3 "is 900, which corresponds to a quasioptimal solution of the problem of finding the maximum value of the function f (x) = x 2 on the interval [0.31].
Davis's genetic algorithm includes the following steps:
1. Initialization of the chromosome population.
2. Evaluation of each chromosome in the population.
3. Creating new chromosomes by modifying and crossing current chromosomes (using mutation and crossing-over operators).
4. Elimination of chromosomes from the population to replace them with new ones.
5. Evaluation of new chromosomes and their inclusion in the population.
6. Check the condition of exhaustion of the time resource allocated for the search for the optimal solution (if time is exhausted, the algorithm is completed and the best chromosome is returned, otherwise go to step 3).
Holland proposed for the genetic algorithm the inversion operator, which is implemented according to the scheme:
1. String (chromosome) B = {b x , b 2 , ..., b L } is chosen randomly from the current population.
2. From the set Y {0,1,2, L + 1} two numbers at 1 and y 2 are randomly selected and the values x 1 = min {y 1 , y 2 } and x 2 = max {y 1 , y are determined 2 }.
3. Из хромосомы В формируется новая хромосома путем ин- -Jверсии (обратного порядка) сегмента, лежащего справа от позиции x 1 и слева от позиции х 2 вхромосоме В. После применения оператора инверсиистрока В примет вид В'={b 1 ,…, b x 1 ,b x 2-1 ,b x 2-2 ,…,b x 1+1 ,b x 2 ,…,b L }.
Например, для строки В={1, 2, 3, 4, 5, 6} при выборе у 1 =6 и y 2 =2 соответственно x 1 =2, x 2 = 6 результатом инверсии будет B ' ={1, 2, 5, 4, 3, 6}.
Операции кроссинговера и мутации, используемые в простом IX, изменяют структуру хромосом, в том числе разрушают удачные фрагменты найденных решений, что уменьшает вероятность нахождения глобального оптимума. Для устранения этого недостатка в генетических алгоритмах используют схемы (схематы или шаблоны), представляющие собой фрагменты решений или хромосом, которые желательно сохранить в процессе эволюции. При использовании схем в генетическом алгоритме вводится новый алфавит {0,1,*}, где * интерпретируется как «имеет значение 1 или 0». Например: схема (*0000) соответствует двум стрингам {10000 и 00000};
- схема (*111*) соответствует четырем строкам {01110, 11110, 01111,11111};
- схема (0*1**) может соответствовать восьми пятизначным стрингам.
В общем случае хромосома длиной L максимально может иметь 3 L схем (шаблонов), но только 2 L различных альтернативных стрингов. Это следует из факта, что схеме (**) в общем случае могут соответствовать 3 2 =9 стрингов, а именно {**, *1, *0, 1*, 0*, 00, 01, 10, 11}, и только 2 2 =4 альтернативные строки {00,01,10,11}, т. е. одной и той же строке может соответствовать несколько схем.
Если в результате работы генетического алгоритма удалось найти схемы типа (11***) и (**111), то применив оператор кроссинговера, можно получить хромосому (11111), обладающую наилучшим значением целевой функции.
Short length circuits are called building blocks. The size of building blocks significantly affects the quality and speed of finding the result. The type of building block is chosen taking into account the specifics of the problem being solved, and their gap in genetic algorithms is allowed only in exceptional cases defined by the user. For example, in the scheme (**** 1) the building block is element 1, and in the scheme (10 ***) it is component element 10.
When using a large number of building blocks, genetic algorithms based on the random generation of populations and chromosomes are promiscuous.
Стационарные генетические алгоритмы отличаются от поколенческих тем, что у первых размер популяции является заданным постоянным параметром, который определяется пользователем, а у вторых размер популяции в последующих генерациях может увеличиваться или уменьшаться.
Процедура удаления лишних хромосом в стационарных и поколенческих генетических алгоритмах основана на эвристических правилах, примерами которых являются следующие:
- случайное равновероятное удаление хромосом;
- удаление хромосом, имеющих худшие значения целевой функции;
- удаление хромосом на основе обратного значения целевой функции;
- удаление хромосом на основе турнирной стратегии.
Следует иметь в виду, что использование в генетических алгоритмах тех или иных эвристик удаления хромосом может повлечь за собой негативные последствия. Например, удаление худших хромосом приводит к преждевременной утрате разнообразия и, как следствие, к попаданию целевой функции в локальный оптимум, а при наличии большого числа хромосом с плохими значениями целевой функции утрачивается направленность поиска, и он превращается в «слепой» поиск.
Comments
To leave a comment
Intelligent Information Systems
Terms: Intelligent Information Systems